Balancing Binary Trees Before Insertion

Using the "Middle Out" Technique

I’m currently working through A Common-Sense Guide to Data Structures and Algorithms. The examples are in Ruby and Python. But since I’m learning Rust, I implement the examples and exercises as a transfer exercise in that programming language.

Node-based data structures such as linked lists, trees, and graphs are chronically harder to implement in Rust than in most other programming languages due to its ownership concept. Having chosen to work on data structures and algorithms in Rust, I was fully aware of the uphill battle I’ve entered. With some help from the very friendly Rust community, I managed to work through chapter 14 on (doubly) linked lists, implementing a Deque in the process.

Today, I wanted to work through chapter 15 on binary trees. I was familiar with most of the content. However, deleting a node from a tree is not so easy, because there are different cases:

1. The node can be a leaf, in which case it just can be dropped.
2. The node can have one child, in which case the sole child is elevated to the current node’s position.
3. The node can have two children, in which case a proper child has to be found among the successors of both children.

The third case even has a special case—at least it’s special in Rust: If the node to be deleted is the root node, the delete() method has to consume the node and to return a new one.

This made me think: When the API has to be designed in a way such that the delete operation returns a fresh tree, why not just build up a fresh tree with the value to be deleted missing? (This of course implies set semantics for the tree: every value is unique. But it could also be done without that restriction.)

It’s Sunday morning, after all, and I’m not feeling like wrestling with the borrow checker today. (Yes, I am a bit of a coward, but I can implement the proper algorithm later.)

But the idea made me think: Is it possible to give the client a benefit in exchange for the performance penalty of building up a fresh tree? When I rebuild the tree from scratch, I could make sure that it comes out balanced afterwards! But how can I pull this off?

But first, let’s introduce the tree data structure.

Binary Tree in Rust

Let’s begin with a new project:

cargo new --lib binary_tree

The binary tree implementation should go into src/binary_tree.rs, and src/lib.rs should make use of that module:

pub mod binary_tree;

A Node shall contain a value with a generic type and a child on both the left and right side (src/binary_tree.rs):

pub struct Node<T: Clone + Ord> {
    value: T,
    left: Option<Box<Node<T>>>,
    right: Option<Box<Node<T>>>,
}

The node’s value type must both implement the Clone and Ord trait, so that the values can be cloned and sorted. The left and right children are wrapped in an Option because they could be missing, and in a Box so that the child nodes are placed on the heap, breaking the endless cycle of nodes containing nodes.

There won’t be a Tree structure, but the client is expected to use the root node as a reference to the entire tree. For Node, a couple of operations shall be implemented. Let’s start with a new associated function (the following methods are all placed in the same impl block in src/binary_tree.rs):

impl<T> Node<T>
where
    T: Clone + Ord,
{
    pub fn new(value: T) -> Self {
        Node {
            value,
            left: None,
            right: None,
        }
    }
}

This allows us to create a new node as follows:

let node = Node::new(7);

Children shall be inserted at their proper place. For a binary search tree, values smaller than the current node’s value go to the left side, values greater than the current node’s value go to the right side:

pub fn insert(&mut self, value: T) {
    match value.cmp(&self.value) {
        Ordering::Less => match &mut self.left {
            Some(ref mut node) => node.insert(value),
            None => self.left = Some(Box::new(Self::new(value))),
        },
        Ordering::Greater => match &mut self.right {
            Some(ref mut node) => node.insert(value),
            None => self.right = Some(Box::new(Self::new(value))),
        },
        Ordering::Equal => (),
    }
}

Make sure to import the Ordering enum for this purpose:

use std::cmp::Ordering;

If the node already has a child on the left/right side, the value shall be inserted further down the tree in the proper direction. If the node has no child at the respective place, it can be inserted directly as a new node. If the value already exists in the tree, it is simply ignored. (We’re working with set semantics here.)

To get the values out, the following method traverses the tree and returns its values in order, i.e. sorted:

pub fn get_values(&self) -> Vec<T> {
    let left = match &self.left {
        Some(node) => node.get_values(),
        None => Vec::new(),
    };
    let middle = vec![self.value.clone()];
    let right = match &self.right {
        Some(node) => node.get_values(),
        None => Vec::new(),
    };
    [left, middle, right].concat()
}

That’s enough code for some automated tests, to be written in src/binary_tree.rs, too:

#[cfg(test)]
pub mod tests {
    use super::*;

    #[test]
    fn test_get_values() {
        let mut root: Node<usize> = Node::new(4);
        root.insert(2);
        root.insert(1);
        root.insert(3);
        root.insert(6);
        root.insert(5);
        root.insert(7);

        let expected: Vec<usize> = (1..=7).collect();
        let actual = root.get_values();
        assert_eq!(actual, expected);
    }
}

A tree is built up with values from 1 up to 7 (inclusive). The insertion order was hand-crafted carefully so that we end up with a balanced tree:

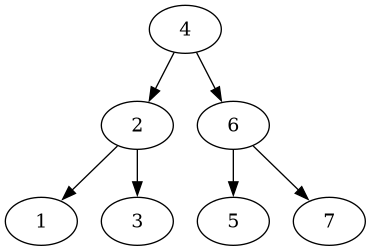
This yields the values in an ascending order.

Deleting a Node, Rebuilding the Tree

Deleting a node by its value is very simple if a new tree is built up in the process. Let’s re-use the existing methods to implement delete() (again in the impl block in src/binary_tree.rs):

pub fn delete(&self, value: &T) -> Option<Self> {
    let values = self.get_values();
    let values: Vec<T> = values.into_iter().filter(|v| v != value).collect();
    if values.is_empty() {
        None
    } else {
        let mut root = Self::new(values[0].clone());
        for v in &values[1..] {
            root.insert(v.clone());
        }
        Some(root)
    }
}

The method expects a Node reference, so nothing is modified, but a fresh tree is returned. If the value to be deleted is the current node’s value, and if the current node has no children, an empty tree or no tree is returned, thus Option as the return type.

The values are obtained using the get_values() method from before. Now the value to be removed is filtered out. With the remaining values, a new tree is built up.

This is very simple. But since get_values() returns the items in order, i.e. sorted ascendingly, the resulting tree (or “tree”) will look like this (e.g. after removing the node with value 3):

Not much of a binary tree, is it? Lookups will take O(n) instead of O(log n) steps.

So the values must be handed over to the new tree in a different manner. There are two options I’d like to demonstrate:

1. The values are obtained in pre-order.
2. The values are re-sorted in middle out order.

Pre-Order Traversal

If the tree is already in a decent shape to begin with, obtaining the values in a way such that the value comes before its children’s values will yield decent results.

Let’s extend the get_values() method by telling it in what order the nodes shall be traversed. For that purpose, an enum is created:

enum Traversal {
    InOrder,
    PreOrder,
}

There’s also a post order, which isn’t relevant for our use case. Now get_values() shall be extended as follows:

pub fn get_values(&self, order: &Traversal) -> Vec<T> {
    let left = match &self.left {
        Some(node) => node.get_values(order),
        None => Vec::new(),
    };
    let middle = vec![self.value.clone()];
    let right = match &self.right {
        Some(node) => node.get_values(order),
        None => Vec::new(),
    };
    match order {
        Traversal::InOrder => [left, middle, right].concat(),
        Traversal::PreOrder => [middle, left, right].concat(),
    }
}

The order is expected as a Traversal reference and handed down to the child nodes. The left, right, and middle parts are still established in the same way. However, upon returning the result, the resulting vector is constructed in a different order depending on the Traversal variant.

Let’s extend the test to verify the behaviour:

#[test]
fn test_get_values() {
    let mut root: Node<usize> = Node::new(4);
    root.insert(2);
    root.insert(1);
    root.insert(3);
    root.insert(6);
    root.insert(5);
    root.insert(7);

    let expected: Vec<usize> = (1..=7).collect();
    let actual = root.get_values(&Traversal::InOrder);
    assert_eq!(actual, expected);

    let expected: Vec<usize> = vec![4, 2, 1, 3, 6, 5, 7];
    let actual = root.get_values(&Traversal::PreOrder);
    assert_eq!(actual, expected);
}

If the elements are inserted in that particular order, we’ll get back the original tree.

But let’s extend the delete method, which was the actual purpose of this digression:

pub fn delete(&self, value: &T) -> Option<Self> {
    let values = self.get_values(&Traversal::PreOrder); // NOTE: order specified
    let values: Vec<T> = values.into_iter().filter(|v| v != value).collect();
    if values.is_empty() {
        None
    } else {
        let mut root = Self::new(values[0].clone());
        for v in &values[1..] {
            root.insert(v.clone());
        }
        Some(root)
    }
}

The only modification is the way get_values() is being called: with PreOrder specified as the Traversal order.

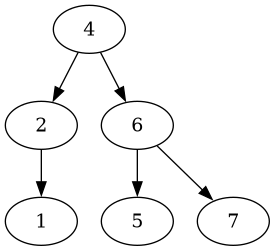
Let’s test the deletion of a leaf:

fn test_delete_leaf() {
    let mut root: Node<usize> = Node::new(4);
    root.insert(2);
    root.insert(1);
    root.insert(3);
    root.insert(6);
    root.insert(5);
    root.insert(7);

    let tree = root.delete(&3).unwrap();
    assert_eq!(tree.get_values(&Traversal::InOrder), vec![1, 2, 4, 5, 6, 7]);
}

Which yields a pretty decent tree:

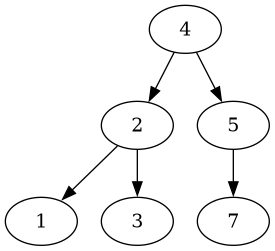
Now let’s delete the root node’s right child:

#[test]
fn test_delete_middle() {
    let mut root: Node<usize> = Node::new(4);
    root.insert(2);
    root.insert(1);
    root.insert(3);
    root.insert(6);
    root.insert(5);
    root.insert(7);

    let tree = root.delete(&6).unwrap();
    assert_eq!(tree.get_values(&Traversal::InOrder), vec![1, 2, 3, 4, 5, 7]);
}

Which also yields a decent tree:

Let’s try deleting the root node:

#[test]
fn test_delete_root() {
    let mut root: Node<usize> = Node::new(4);
    root.insert(2);
    root.insert(1);
    root.insert(3);
    root.insert(6);
    root.insert(5);
    root.insert(7);

    let tree = root.delete(&4).unwrap();
    assert_eq!(tree.get_values(&Traversal::InOrder), vec![1, 2, 3, 5, 6, 7]);
}

That doesn’t look so nice anymore:

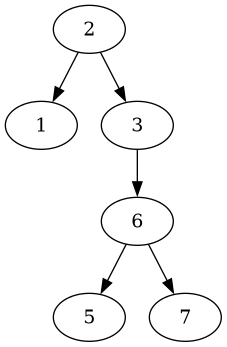
This tree has now four levels, but its 6 elements could easily fit on three.

It would be nice to have a way to pre-order the values in a way such that the tree will be perfectly balanced in the first place. Enter middle out!

Middle Out

I’m such an idiot. Middle out. Middle out! MIDDLE OUT!"

— Richard Hendricks, Silicon Valley (Season 1, Episode 8)

Here’s how the values can be put in an order that will yield a balanced tree:

1. Obtain the tree’s values in order.
2. Split the list in the middle; return the median element and the list on the left (smaller elements) and on the right (bigger elements).
3. Process the sublists in the same way, thereby adding their median values to a sequence, until all remaining sublists are empty.
4. The sequence of median values can now be inserted into the tree.

The values are extracted from the sequence middle out, so to speak.

Let’s create a new module in src/middle_out.rs, which is to be referred in src/lib.rs as follows:

pub mod binary_tree;
pub mod middle_out;

The middle_out() function shall expect an array of values and return them in proper insertion order as a vector of the same type (src/middle_out.rs):

pub fn middle_out<T: Ord + Clone>(values: &[T]) -> Vec<T> {
    if values.is_empty() {
        Vec::<T>::new()
    } else {
        do_middle_out(&vec![values.to_vec()], &mut Vec::new())
    }
}

If there are no values, an empty vector is returned. Otherwise, a recursive algorithm with an initially empty accumulator vector is returned, which is defined as follows:

fn do_middle_out<T: Ord + Clone>(splits: &Vec<Vec<T>>, acc: &mut Vec<T>) -> Vec<T> {
    if splits.iter().all(|s| s.is_empty()) {
        return acc.clone();
    }
    let mut remainder = Vec::new();
    for split in splits {
        let (median, splits) = split_median(split);
        if let Some(median) = median {
            acc.push(median.clone());
        }
        for split in splits {
            if !split.is_empty() {
                remainder.push(split);
            }
        }
    }
    do_middle_out(&remainder, acc)
}

A vector of “split” vectors is expected; initially, it’s only a single vector. If there are only empty split vectors, all the median values have been extracted in proper order, and the accumulator is returned as the result.

As long as there are non-empty split vectors, both the median and the left/right sub-vectors of the split vector is computed. The found median is added to the accumulator. The newly found split vectors are added to a remainder, which is then processed (tail-)recursively.

The split_median() function is implemented as follows:

fn split_median<T: Ord + Clone>(values: &[T]) -> (Option<T>, Vec<Vec<T>>) {
    let n = values.len();
    if n == 0 {
        (None, Vec::new())
    } else if n == 1 {
        (Some(values[0].clone()), Vec::new())
    } else {
        let mut values = values.to_owned();
        values.sort();
        let m = if n % 2 == 0 { n / 2 - 1 } else { n / 2 };
        let median = &values[m];
        let left = values[0..m].to_owned();
        let right = values[m + 1..n].to_owned();
        (Some(median.clone()), vec![left, right])
    }
}

There are three cases to be covered:

1. If there are no elements, neither median nor split vectors are returned.
2. If there is one value, it is returned as the median, but no split vectors are returned.
3. If there are multiple elements, they are first sorted. Then the median element is extracted, and the slices on the left and right of it are extracted. Both median and slices are returned.

Let’s verify this algorithm with some test cases.

First, an empty vector shall yield an empty vector:

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_middle_out_empty() {
        assert_eq!(middle_out(&Vec::<usize>::new()), Vec::new());
    }
}

Second, the algorithm must work with an even number of elements (to be placed in the above test module, too):

#[test]
fn test_middle_out_small() {
    assert_eq!(
        middle_out(&(1..=8).collect::<Vec<usize>>()),
        vec![4, 2, 6, 1, 3, 5, 7, 8]
    );
}

Inserting the values in this order will yield this nicely balanced tree:

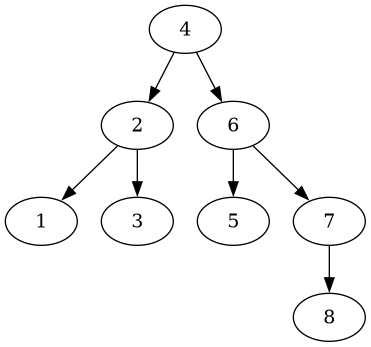
Third, if an odd number of elements is used, the tree shall be balanced, too:

#[test]
fn test_middle_out_big() {
    assert_eq!(
        middle_out(&(0..=14).collect::<Vec<usize>>()),
        vec![7, 3, 11, 1, 5, 9, 13, 0, 2, 4, 6, 8, 10, 12, 14]
    );
}

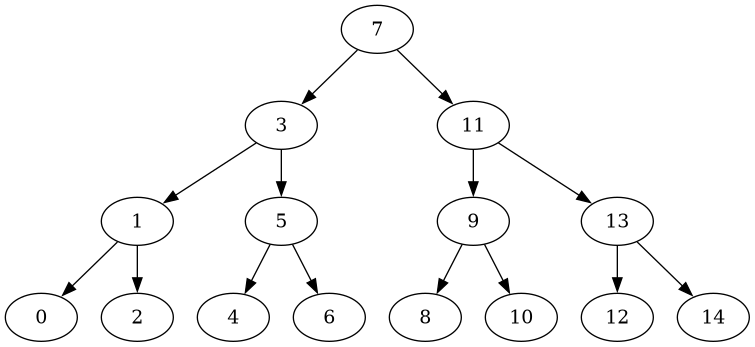
Again, this insertion order yields a balanced tree:

Let’s integrate this functionality into the tree module!

Wrapping Up

Back to the binary_tree module, let’s import the middle_out() function:

use crate::middle_out::middle_out;

The delete() method shall be extended as follows:

    pub fn delete(&self, value: &T) -> Option<Self> {
        let values = self.get_values(&Traversal::InOrder); // NOTE: back to InOrder
        let values: Vec<T> = values.into_iter().filter(|v| v != value).collect();
        let values = middle_out(&values); // NOTE: added line
        if values.is_empty() {
            None
        } else {
            let mut root = Self::new(values[0].clone());
            for v in &values[1..] {
                root.insert(v.clone());
            }
            Some(root)
        }
    }

The values are retrieved in order again. Depending on the sorting algorithm used by middle_out, ordering a pre-ordered vector might be faster than an unordered one. The values are then re-arranged as discussed by calling the middle_out() function.

Let’s check the effects on the delete operations again, starting from this tree:

First, let’s delete the leaf 3, which yields the following tree:

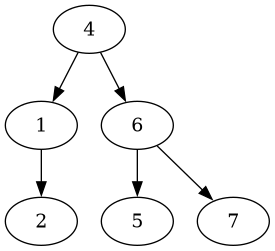
The tree is still balanced, but has a slightly different layout.

Second, let’s delete the middle node with the value 6, which yields this tree:

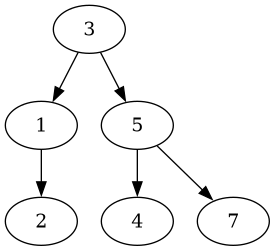
This tree is also still balanced, but also looks a bit different.

Third, let’s delete the root node, which yields this tree:

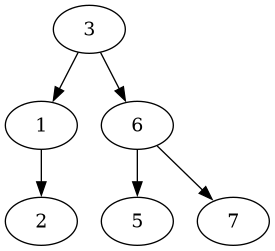
Unlike as before, after deleting the root node, a balanced tree is returned.

So middle out really is a thing!

Conclusion

Dealing with node-based data structures doesn’t have to be a hassle in Rust when one is willing to sacrifice some performance and to re-build data structures instead of modifying them in-place.

Binary trees can be traversed in different orders. The in order traversal yields a sequence of (ascendingly) ordered values. The pre-order traversal yields a sequence with the upper level values of the tree before the lower level ones.

To pre-establish an insertion order that will yield a balanced binary tree, the in order sequence of values can be split up into a left side, a median, and a right side. The resulting medians are added to a resulting sequence of items to be inserted; the process is repeated until the resulting split sequences become all empty. I called this algorithm middle out.

The source code can be obtained from GitHub.